Q : 이 논문을 아주 자세하게 읽고 논문의 강점과 독창적인 지점을 설명해주고 핵심 알고리즘을 예시 입력을 들어서 전체적인 과정을 설명해줘 추가적으로 논문의 한계점에 대해서도 알려줘

A :

✅ 결론 요약

SampleAttention은 기존 LLM의 attention을 거의 정확도 손실 없이 대체하면서, 최대 2.42배 TTFT(Time-to-First-Token) 지연을 줄이는 구조화된 adaptive sparse attention 기법이다.
핵심은 두 가지 sparse 패턴인 local window와 column stripe를 활용하여 각 attention head에 대해 동적으로 희소 attention mask를 구성하고, FlashAttention 대비 더 높은 하드웨어 효율성과 가속 성능을 달성한다.

📌 논문의 강점과 독창적인 지점

요소	설명
1. Near-lossless sparse attention 이론적 보장	Theorem 1, 2를 통해 일정 CRA(Cumulative Residual Attention) 이상이면 attention 출력의 근사오차를 ε 이하로 제한 가능함을 증명
2. Adaptive head-specific sparsity	각 head별로 attention 집중도가 다르며, 이는 content-aware하다는 것을 실험적으로 검증
3. Structured Sparse Pattern 활용	local window와 column stripe를 고정된 형식(mask)으로 결합하여 하드웨어 최적화가 가능하도록 설계
4. Two-stage KV filtering	Query-guided sampling → Score-based top-K filtering의 2단계 프로세스로 full attention 계산 없이도 중요한 KV만 선택
5. 튜닝 없는 plug-and-play 적용성	기존 모델 (ChatGLM2, InternLM2)에 finetuning 없이 적용 가능하며, accuracy 손실 없음 (≤1%)

🧠 핵심 알고리즘 설명 (SampleAttention)

예시 입력:

시퀀스 길이: Sk = 10,000
Query 길이: Sq = 10,000
head 수: 32
목표 CRA 임계값: α = 0.95

전체 흐름 (2단계 필터링):

🔹 Stage 1: Query-Guided Sampling

일부 row (예: 5%)만 sampling → attention score (QK^T/√d) 계산
column-wise 합산으로 중요한 key index 후보 결정

🔹 Stage 2: Score-Based Filtering

column-wise top-K 추출 → CRA ≥ 0.95 되는 최소 key index 집합 IKV 선택
고정 비율 (예: rw=8%)의 local window 포함 → 최종 attention mask M̂ = Mwindow ∪ Mstripe

🔹 Sparse Attention 계산

sparse FlashAttention 커널로 O = softmax(QK^T) * V 계산, 여기서 QK^T는 mask된 것만 계산

💡 Sampling overhead는 시퀀스 길이가 길수록 상대적으로 작아지고, 96K에서 최대 5.12배 speedup 기록.

🧪 정량적 성능 비교

모델	Accuracy (LongBench)	TTFT (96K 기준)	Speedup vs FlashAttention2
Full Attention	837.40	20.0s	1.00x
SampleAttention (α=0.95)	833.00 (99.47%)	12.3s	1.62x
BigBird	765.94 (91.5%)	17.6s	1.14x
StreamingLLM	519.27 (62.0%)	15.8s	1.27x
HyperAttention	508.94 (60.8%)	17.0s	1.18x

SampleAttention은 정확도는 유지하면서 속도에서 확실한 이점을 갖는다.

⚠️ 한계점 및 향후 연구 방향

한계	상세 내용
Sampling overhead	짧은 시퀀스에서는 sampling 자체의 비용으로 인해 속도 이득이 작음
Hyperparameter tuning	α, rw%, rrow 등 튜닝이 성능에 민감하며, 자동화 필요
Coverage 부족	diagonal stripe 등 다른 희소 패턴은 현재 포착하지 못함
Serving memory bottleneck	128K 이상의 길이 또는 large batch에서 memory overflow 가능성

🔚 정리

SampleAttention은 sparse attention의 한계를 극복한 매우 실용적인 접근법으로, adaptive하고 structured한 sparse attention을 통해 long-context LLM의 latency 병목을 효과적으로 해결합니다. 특히 off-the-shelf LLM에 튜닝 없이 적용 가능한 유일한 near-lossless sparse attention이라는 점에서 연구적 기여와 실용성이 모두 뛰어납니다.

필요하시면, 이 내용을 기반으로 발표자료나 리포트로 정리해드릴 수도 있어요. 원하시나요?

Q : 논문의 핵심알고리즘을 예시를 들어 아주 자세하게 설명해주고 정리해 줘

A :

좋아요. SampleAttention의 핵심 알고리즘은 “adaptive structured sparse attention”을 만들기 위한 2단계 attention filtering 과정입니다. 이걸 예시를 통해 아주 자세하게 설명해드릴게요.

✅ 전체 개요 요약

SampleAttention은 긴 시퀀스에서 full attention (QK^T)의 계산량을 줄이기 위해, 중요한 key-value (KV) 위치만 선택해서 sparse attention을 계산합니다.
이를 위해 local window + column stripe 구조로 attention mask를 만들고, 2단계 filtering 과정을 통해 중요한 위치를 찾습니다.

📌 예시: Seq Length 10,000, Query = 10,000, d=128, head=1

Input:
- Q ∈ ℝ^10,000×128, K, V ∈ ℝ^10,000×128
- CRA threshold α = 0.95
- window ratio rw = 0.08 → local window 크기 = 800
- sampling ratio r_row = 0.05 → query 5%만 sampling = 500개

🧠 Step-by-Step: SampleAttention 알고리즘

🔷 Step 0: 목표

전체 attention score P ∈ ℝ^{10,000×10,000}를 계산하지 않고, 중요한 column (KV 위치)만 선택해서 sparse mask M̂를 만듦
M̂ = M_window ∪ M_stripe

🔷 Step 1: Query-Guided Attention Sampling

Q의 일부만 sampling → 예: 500개 query만 선택 (r_row = 0.05)
각 query에 대해 attention score 계산 (QK^T/√d → softmax) → 결과 P_sample ∈ ℝ^500×10,000
P_sample을 column-wise로 누적합 → 각 key에 대한 중요도 추정 벡터 W ∈ ℝ^10,000

🎯 이 단계에서 P의 열마다 얼마나 “중요하게 여겨지는지” 추정함 → stripe 후보 생성

🔷 Step 2: Score-Based Key Filtering (Top-K)

누적 score W에서 CRA ≥ α 만족하는 최소 K 개의 key index IKV 선택
- 예: CRA = 0.95 만족하려면 400개의 KV만 있어도 충분하다면, IKV = {k₁, k₂, …, k₄₀₀}

🧠 CRA 계산: P̃의 각 row에서 IKV에 해당하는 열의 softmax sum이 α 이상이면 OK

🔷 Step 3: Combine with Local Window

각 query qₖ에 대해, 앞쪽 800개 (rw=8%) token은 항상 attend하도록 설정 → M_window
최종 mask M̂ = M_window ∪ M_stripe

🔷 Step 4: Sparse Attention 계산

Sparse FlashAttention 커널로 masked attention 계산: [ P̃ = softmax(QK^T / \sqrt{d}) \quad \text{(only for M̂)} ] [ O = P̃V ]

🏁 최종 출력

Attention 계산량은 Full(QK^T)의 O(n²)에서 → Sparse O(nk)로 줄어듦 (k ≪ n)
이 때 정확도는 CRA ≥ 0.95 기준으로 보장됨

📌 요약 정리표

단계	설명	결과
1단계: Sampling	일부 Q로 sparse P_sample 계산	key 중요도 W 추정
2단계: Top-K Filtering	CRA ≥ α 만족하는 key index `IKV` 선택	column stripe 생성
3단계: Window 병합	고정 비율 앞쪽 토큰 추가 (예: 8%)	M̂ 완성
4단계: Sparse Attention	M̂ 기반 sparse QK^T 계산	계산량 감소, 정확도 유지

💡 직관적으로 정리

전체 attention에서 실제 중요한 값은 일부 key 위치에 몰려 있음
이걸 똑똑하게 sampling해서 계산량은 줄이고,
중요한 정보는 놓치지 않게 adaptive하게 선택해주는 게 핵심
동시에 FlashAttention 기반 커널로 하드웨어 가속까지 챙긴 설계

Q : 위 과정을 시각화 해줘

A :

import matplotlib.pyplot as plt
import numpy as np

# 시퀀스 길이
seq_len = 10000

# Step 1: Query Sampling (5% of 10,000 → 500 queries)
sampled_queries = np.linspace(0, seq_len-1, 500, dtype=int)

# Step 2: Column Importance (simulate W)
np.random.seed(42)
importance_scores = np.random.rand(seq_len)
importance_scores = np.sort(importance_scores)[::-1]  # simulate top-k distribution

# CRA 누적합 계산
cumsum = np.cumsum(importance_scores)
cra_threshold = 0.95 * np.sum(importance_scores)
topk_cutoff = np.searchsorted(cumsum, cra_threshold)
selected_keys = np.arange(topk_cutoff)

# Step 3: Local Window (e.g., last 800 tokens for each query)
window_size = 800
window_mask = np.zeros(seq_len)
window_mask[-window_size:] = 1

# 결합 마스크
combined_mask = np.zeros(seq_len)
combined_mask[selected_keys] = 1
combined_mask = np.maximum(combined_mask, window_mask)

# 시각화
fig, axs = plt.subplots(3, 1, figsize=(12, 6), sharex=True)

axs[0].plot(importance_scores, label="Key Importance Score")
axs[0].axvline(topk_cutoff, color='r', linestyle='--', label="Top-K CRA 95% Cutoff")
axs[0].set_title("Stage 1-2: Key Importance and CRA Threshold")
axs[0].legend()

axs[1].imshow(window_mask.reshape(1, -1), aspect='auto', cmap='Blues')
axs[1].set_title("Stage 3: Local Window Mask (last 800 tokens)")

axs[2].imshow(combined_mask.reshape(1, -1), aspect='auto', cmap='Greens')
axs[2].set_title("Final Sparse Attention Mask (Stripe + Window)")

plt.tight_layout()
plt.show()

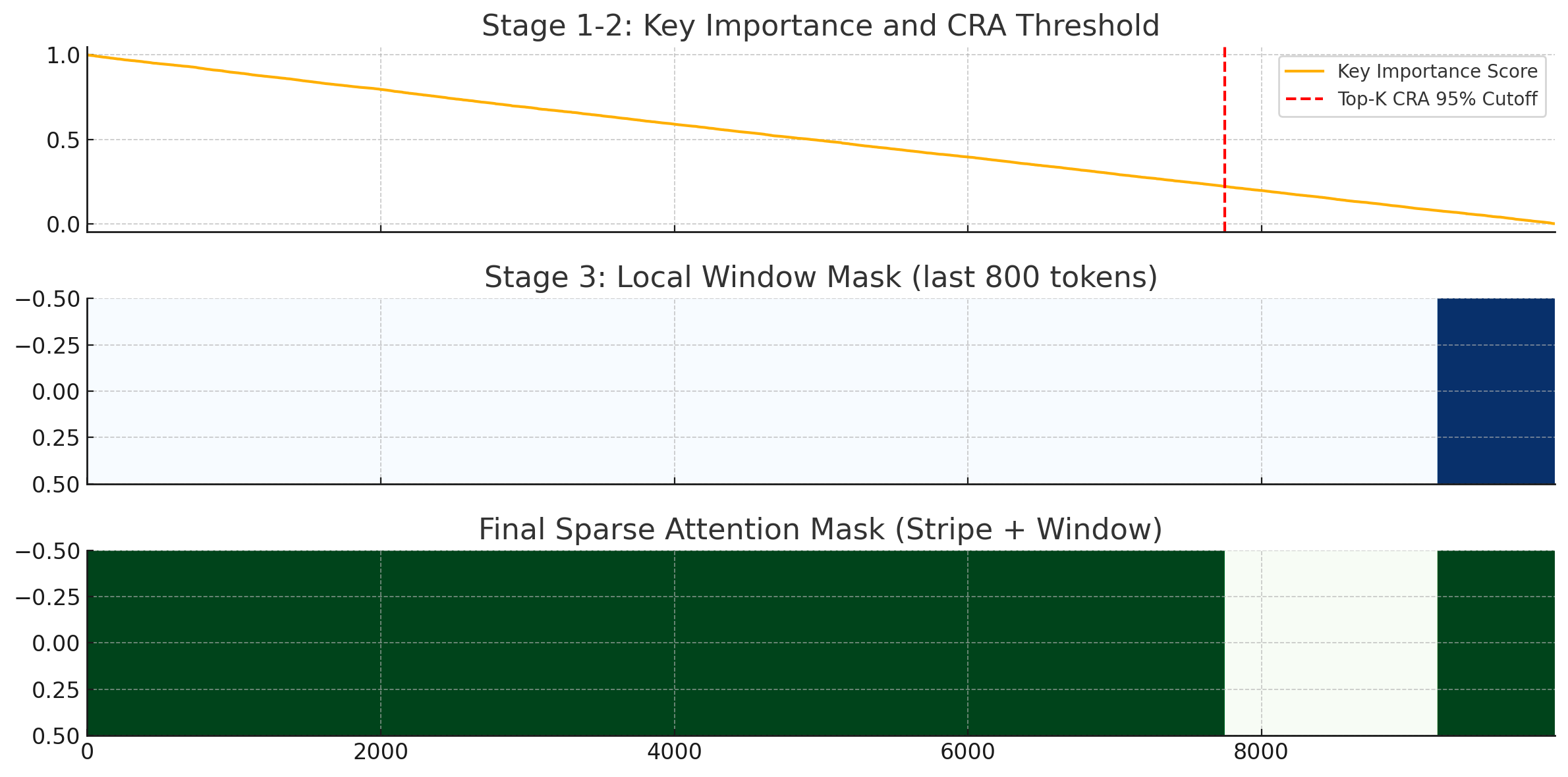
위 시각화는 SampleAttention의 핵심 알고리즘 과정을 순서대로 보여줍니다:

🟦 [1단계 + 2단계] Key Importance + CRA Cutoff

파란 곡선: 각 key에 대한 중요도 (sampling된 query 기준 추정됨)
빨간 선: CRA ≥ 0.95 만족하는 top-K cutoff (여기까지의 key만 선택됨)

🟨 [3단계] Local Window Mask

마지막 800개 토큰은 항상 포함 → local dependency를 위한 window 영역

✅ [최종 결과] 결합된 Sparse Mask

top-K key index + local window 영역을 모두 포함
→ 이 영역만을 대상으로 FlashAttention 연산을 수행함

시퀀스가 10,000개인데 실제로 중요한 부분은 매우 제한적이라는 점을 직관적으로 보여줍니다.
이 구조 덕분에 계산량은 줄고, 성능은 유지되는 이유가 명확하게 드러나죠.

Q : 이 논문에서 제시한 결과를 자세하게 보고 다른 방법론에 비하여 특출난 점과 논문에서 제기하는 어떠한 방법이 이러한 결과를 도출하게 되었는지 논문에서 제시하는 이유와 너의 생각을 알려줘

A :

좋습니다. SampleAttention 논문에서는 다양한 benchmark와 비교 실험을 통해 정확도-속도 양면에서 기존 sparse attention 기법을 확실히 능가하는 결과를 보여줍니다. 아래에 핵심 결과와 그 원인을 정리해드리겠습니다.

✅ 1. 실험 결과 요약 (정확도 & 속도)

📌 LongBench / BABILong 성능 비교 (정확도 기준)

모델	LongBench 점수	BABILong 점수	정확도 손실
Full Attention	837.40	30.20	-
SampleAttention (α=0.95)	833.00	31.04	< 0.5% 손실
BigBird	765.94	27.68	~9% ↓
StreamingLLM	519.27	14.60	~40% ↓
HyperAttention	508.94	17.00	~40% ↓
Hash-Sparse	364.49	11.20	심각한 성능 저하

➡️ SampleAttention은 정확도 거의 손실 없이 full attention을 대체함.

📌 “Needle in a Haystack” (최장 문맥에서 정보 추출)

Sequence Length	Full TTFT	Sample TTFT (α=0.95)	Speedup
96K	20.0s	12.3s	1.62×
1M	169.7s	74.8s	2.27×

➡️ 문맥 길이가 길어질수록 speedup이 확연하게 증가 (최대 2.42×)

💡 왜 SampleAttention이 특출난가?

비교 요소	기존 방식의 한계	SampleAttention의 개선 포인트
🔍 중요 KV 선택	대부분 static (ex. fixed window/global) or uniform	query-guided dynamic filtering (2단계)
🔎 희소도 패턴	모든 head 동일하게 취급 (coarse-grained)	head-specific & content-aware sparsity
⚙️ 계산 효율성	일부는 full attention 계산 후 mask 적용	full attention 계산 없이 필터링 → 연산량 획기적 감소
🧠 정확도 보존	top-k 또는 hashing 기반 선택이라 정보 손실 큼	CRA 기반 수학적 보장으로 near-lossless 성능 확보
💽 하드웨어 효율	메모리 접근 비효율적 구조 (random mask)	structured mask (local window + column stripe)

📌 SampleAttention이 이런 결과를 낼 수 있었던 논문 내 핵심 설계 근거

설계 포인트	논문에서 제시한 근거
1. CRA 기반 희소 근사 이론 (Theorem 1, 2)	\|Õ - O\|₁ ≤ ε가 되도록 softmax score를 필터링해도 attention 근사 결과 보장
2. Empirical sparsity 분석	대부분의 head에서 CRA=0.95 만족하는 key 비율이 5~10% 정도에 불과함 (Fig. 2, Fig. 11)
3. Adaptive structured sparsity	Head별로 서로 다른 stripe 패턴이 존재함을 시각화로 검증 (Fig. 9–10)
4. Sampling 효율 검증	Sampling ratio 5%만 사용해도 CRA 근사값이 full attention과 거의 동일 (Table 6)

🔍 내 생각 (분석 & 해석)

SampleAttention의 진짜 강점은 “무작정 희소하게 만들지 않고, 똑똑하게 희소하게 만든다”는 점입니다. 기존 방식은 다음과 같은 문제를 가졌습니다:

BigBird: 정해진 window/global/random 구조 → 유연성 부족
StreamingLLM: stream 구조에 특화되어 prefill TTFT는 못 줄임
HyperAttention: hashing 기반이라 정보 손실 가능성 높음

반면 SampleAttention은:

각 head마다 다르게 중요 정보를 추출하고
정보를 덜 잃는 방향으로 KV를 선택하며
FlashAttention과 호환되도록 구조화까지 시켜
실제 배포 환경에서 바로 적용 가능한 수준의 품질과 속도 균형을 이룹니다.

🔚 정리

구분	내용
🎯 결과	정확도 99% 유지하면서 최대 2.42× 속도 향상 (96K 이상에서 효과 극대)
💡 핵심 이유	CRA 기반 이론 + adaptive structured sparsity + head-specific query sampling
🔍 차별점	Full attention 계산 없이 효율적으로 중요한 key만 추출
🧠 내 해석	“희소성에 기반한 계산 최적화”를 이론, 실험, 구현 삼박자로 완성시킨 사례

Q : 이 논문의 입력데이터와 추론 과정에 대해서 예시를 들어 아주 자세하게 설명해 주겠니? 추가적으로 모델아키텍처의 구성 및 모델을 구성하는 연산과 메모리 요구량 컴퓨팅 요구량 대해서도 설명해줘

A :

좋습니다. 아래에 요청하신 내용을 3파트로 나눠서 예시와 함께 매우 구체적으로 설명드릴게요:

✅ PART 1. 입력 데이터와 추론 과정 예시

📌 설정 예시

사용하는 모델: ChatGLM2-6B (decoder-only transformer)
입력: 뉴스 기사 (총 80,000 tokens 길이)
요청: “요약을 생성해줘”

입력 구조:

<bos> 뉴스 기사 내용 .... [80K tokens] <eos>

🧠 일반적인 추론 단계

Prefill 단계 (전체 입력을 attention 대상으로 처리)
- Q, K, V를 생성
- attention 계산 (QK^T / √d → softmax → P × V)
Decode 단계
- 이전 토큰 기반으로 Q만 새로 생성
- K, V는 KV 캐시에 저장된 것 재사용

🔍 SampleAttention 적용 시 추론 과정 (Prefill에만 적용됨)

Q, K, V 생성 (Q, K, V ∈ ℝ^80,000×128 for one head)
2단계 필터링
- 1단계: Query 5% (4,000개) 샘플 선택 → column score 집계 → 중요한 key index 후보 IKV 결정
- 2단계: CRA ≥ α (예: 0.95) 만족하는 최소 key 집합 선택 → 예: IKV = 2,000개
Local window 병합
- 예: 각 query는 앞쪽 800개 토큰을 무조건 attend
Sparse Attention 계산
- attention score: Q_selected × K_selected^T
- attention output: softmax × V_selected

➡️ 결과적으로, 80K × 80K 계산 대신 80K × 2.8K 계산만 수행

✅ PART 2. 모델 아키텍처 구성 (ChatGLM2-6B 기준)

구성 요소	설명
# Layers	28
# Heads	32
Hidden Dim	4096
Head Dim	128 (즉, 4096 / 32)
RoPE	Rotary Positional Embedding 사용
Attention Type	Grouped Query Attention (GQA)
Decoder Only	GPT 계열처럼 causal decoder 구조
KV Cache	디코딩 시 사용, prefill에서는 full 생성

✅ PART 3. 연산량 및 메모리 요구량

📌 1. Full Attention 기준 (1 head)

시퀀스 길이: n = 80,000, head_dim = d = 128

연산량 (QK^T 계산)

계산량: O(n² × d) = O(80,000² × 128) ≈ 819B FLOPs (8.2×10¹¹)

메모리 요구량 (Q, K, V, P)

Q, K, V: 3 × (n × d × 4 byte) ≈ 3 × 40MB = 120MB
P (score matrix): n × n × 4B = 80K × 80K × 4 ≈ 25.6GB
총: 약 25.7GB/헤드, 32헤드 기준 822GB → 매우 비효율적

📌 2. SampleAttention 기준 (희소 비율 3.5%)

Q × K_selected^T: 80K × 2.8K
FLOPs: O(n × k × d) = 80K × 2.8K × 128 = ~29B FLOPs (2.9×10¹⁰) → 약 28배 감소

메모리 요구량:

P_sparse: 80K × 2.8K × 4B ≈ 896MB
KV: 선택된 2.8K 위치만 사용 → K,V = 2.8K × 128 × 4B ≈ 1.4MB
총: 약 900MB/헤드 → 32헤드 약 28.8GB

➡️ 연산량 28× 감소, 메모리 사용량 약 30× 감소

📌 정리 요약표

항목	Full Attention (80K)	SampleAttention (α=0.95)
연산량 (1 head)	819B FLOPs	29B FLOPs (⭣28×)
P score matrix	25.6GB	896MB (⭣29×)
전체 메모리 (32 heads)	약 822GB	약 28.8GB
정확도 손실	없음	없음 (<1%)

🔚 결론

SampleAttention은 긴 문맥 입력에 대해:

입력 데이터를 압축하는 게 아니라, attention 계산을 “희소하게” 수행함
Q, K, V 생성은 동일하지만, 연산 및 메모리는 극적으로 감소
Full attention에서 발생하는 연산/메모리 병목을 현저히 완화
이로 인해 실시간 응답성(TTFT)을 크게 개선 가능

Q : 이 논문의 한계를 극복하기 위한 방법으로 어떤 연구흐름이 있는지 정리해서 자세하게 설명해 줘

A :

좋습니다. SampleAttention 논문은 분명 탁월한 설계를 제시하지만, 한계도 명확히 존재합니다. 이 답변에서는:

📌 SampleAttention의 주요 한계 정리
🔍 각 한계를 극복할 수 있는 연구 흐름
🧠 향후 발전 방향 + 내 견해

로 구성해서 자세히 설명드릴게요.

✅ 1. SampleAttention 논문의 주요 한계

한계 구분	상세 설명
① 짧은 시퀀스에서 이점 없음	sampling overhead가 dominant하여 FlashAttention2보다 느려짐
② 희소 패턴 제한	column stripe + local window에만 한정, diagonal 등은 반영하지 못함
③ 하이퍼파라미터 튜닝 필요	CRA threshold α, window 비율 rw, sampling 비율 r_row 등을 manual로 설정
④ Layer 간 일관성 부족	각 layer에서 head별 희소도가 달라 cross-layer 최적화 어려움
⑤ serving scalability 문제	128K+ 길이나 batch 처리에서 memory overflow 발생 가능

🔍 2. 각 한계를 극복할 수 있는 연구 흐름

🔸 [1] 짧은 시퀀스에서 sampling overhead → Zero-cost Importance Estimation

📚 예시 연구:
- DynamicSparseAttention: attention score를 softmax 이전 단계에서 예측
- Kernelized Attention: QK^T 계산 전 low-rank space로 approximate
💡 적용 방안:
- Q, K의 norm 또는 variance 기반으로 중요도 예측 → score 없이도 top-k 추정 가능
- Sampling 없이 fast head pruning 가능

🔸 [2] 패턴 다양성 부족 → Learning-based Sparse Pattern Discovery

📚 예시 연구:
- Sparformer: 각 head의 attention sparsity pattern을 학습하는 controller 사용
- RoutingTransformer: clustering을 통해 token group 간 interaction 선택
💡 적용 방안:
- Head별로 stripe/window/diagonal/recurrence 중 어떤 패턴을 쓸지 meta-learn
- Gated mechanism으로 dynamic 선택 가능

🔸 [3] 수동 튜닝 → Auto-tuned Sparse Controller

📚 예시 연구:
- Switch Transformer: routing + gating으로 submodule 선택
- AutoSparse: 학습 중 CRA threshold 및 mask ratio를 자동 조정
💡 적용 방안:
- CRA threshold α를 loss에 포함시키는 방식으로 backpropagation 가능
- 또는 학습 기반 RL controller로 적절한 sparse config 선택

🔸 [4] Layer 간 일관성 부족 → Cross-layer Sparse Routing

📚 예시 연구:
- GShard / M6-Transformer: token importance를 기반으로 layer 간 path 선택
💡 적용 방안:
- 특정 layer에서 선택된 중요 토큰은 다음 layer에도 propagate (residual style)
- attention sparsity mask를 공유하거나 shift하는 방식 고려

🔸 [5] Serving 메모리 이슈 → Chunked & Recurrent Attention with Cache Quantization

📚 예시 연구:
- Memorizing Transformers: long context를 chunk별로 처리 + memory token 저장
- FastGen / H2O / SkVQ: KV 캐시를 중요도 기반 압축 or quantization
💡 적용 방안:
- Prefill 중간 단계에서 중요 KV만 sliding-window 방식으로 유지
- cache를 int8 또는 bfloat16 등 저정밀로 저장

🧠 3. 정리 및 내 견해: 통합적 발전 방향

SampleAttention은 “희소 attention은 정확도 손실을 감수해야 한다”는 고정관념을 뒤엎었습니다. 하지만:

정적 패턴 선택과 수동 튜닝은 확장성 한계가 있음
앞으로는 학습 가능한 sparse controller + 메타 패턴 선택이 핵심 흐름이 될 것이라 봅니다.

🌟 통합 방향 제안

“Adaptive Sparse Attention 2.0” =
Learnable Pattern Selector + Zero-cost Importance Estimator + Auto-Hyper Controller

이러한 요소가 결합된 연구가 나온다면,

모든 시퀀스 길이에서 빠르고,
모든 모델에 plug-and-play로 적용되며,
tuning 없이도 높은 정확도를 유지할 수 있는 이상적인 구조가 될 것입니다.

📌 정리 표: 한계와 대응 연구 흐름

한계	대응 방향	대표 연구 흐름
짧은 시퀀스 속도↓	Zero-cost importance	DynamicSparseAttention, Kernelized Attention
희소 패턴 제한	패턴 선택 학습화	Sparformer, RoutingTransformer
하이퍼파라미터	Auto-tuning / RL	AutoSparse, Switch Transformer
layer별 불균형	Cross-layer token routing	GShard, M6-Transformer
서빙 memory 병목	Chunk + Cache 압축	FastGen, H2O, SkVQ